在最后的冲刺阶段里，广东公务员考试网接下来都会给大伙儿带来一些省考冲刺干货，今天是数量关系的考试干货。希望能帮到你：

　　1、数字推理思路总结

　　数字推理题型根据数字的规律不同，一般可以分为以下几类，不同的数列做法不一样。

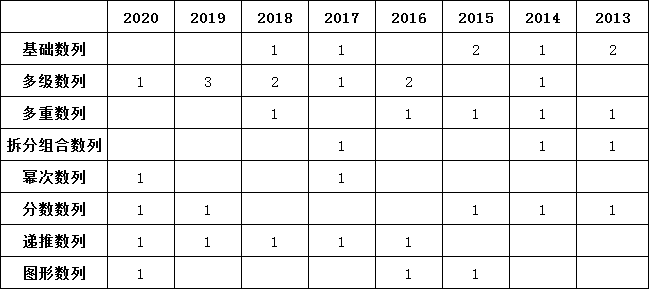
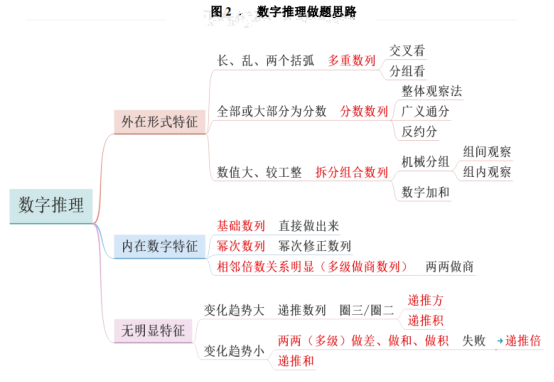
　　基础数列，如“6，14，22，（），38，46”，这是一个公差为8的等差数列，基础数列一般都是8大基本规律。

　　分数数列，分数数列常见的规律有两个，一是后一项的分子、分母由前一项得到，另一中分子是一组数列、分母是一组数列。分数的特点是分子分母可以约分，而题干中给出的分数往往给出的都是最简分数，这使得考生很难之间观察得到规律，需要对其中的一个或者几个分数进行反约分（分子分母同乘一个数）

　　多重数列，特点是项数往往会比较多，规律有以下几个，可能分别是奇数项、偶数项构成一组数列，也可能是相邻的两项（1、2项，3、4项……）两两分组甚至是首尾分组构成数列，如果项数是9或12项，则是三三分组。两两分组考虑两个数字“加减乘除”得到的数字会有规律，三三分组一般是前两项经过某种运算得到第三项。

　　幂次数列，各项都和幂次相关。幂次数列也有两种情况，简单的幂次（所给的数字全是幂次）或者幂次修正（所给的数字在幂次数附近上下波动），幂次数列还喜欢喜欢结合其他数列来考，比如分数数列或者递推数列。

　　多级数列，也是常考数列，最常见的是多级做差和做商数列。二级做差数列，相邻的两项相减，得到差数列会有一定的规律；二级做商数列相邻的两项之间有明显的倍数关系，做商得到的商数列会有一定的规律；常考的还有三级做差数列，一次做差得到差数列没有规律，那就需要对二级差数列再做一次差，得到三级做差数列，这时候会呈现一定的规律。多级做和和多级做积数列几乎没有涉及到，一般不会出现在考试当中。

　　递推数列考得很多，一般分为递推和（差）、递推倍、递推积、和递推方四种，这种数列不一定会单调递增或者递减，数字变化趋势不大考虑递推和，变化趋势相对较大考虑递推倍，变化趋势比较大考虑递推积，变化趋势巨大就要考虑递推方了。常用的方法是圈三看二，一般是相邻的三项或者两项之间有递推的关系（比如第一项+第二项=第三项），也有第一、二项递推第四项等等其他的变型形式。递推数列难度跨越比较大，有可能找到了规律但是没有相应的选项，这是由于考生的思路和命题人的思路不一致，所以这类数列往往需要尝试多次才能找到符合正确答案的规律。

　　机械分组数列（拆分组合数列），这类数列就是“拆”，是位置相关的数列，机械分组数列数字一般位数都很多，目前有过的规律大致有以下几类。三位数居多（也有考过全四位数的），每一项的数字把各位上的数字加和，数字和组成的数列有某种基本规律，或者每个数字内部之间有运算关系（比如每个三位数都是第一个数字+第三个数字=中间的数字）；全是四位数，一般把四位数拆成两个两位数（当成多重数列中的分组数列来做）；还有一些广义上的拆分组合数列，比如带根号的数列，拆成整数+（×）根式的形式，小数数列拆成整数+小数的形式等等。

　　图形数列，也是一类比较难的题目，有九宫格、十二宫格、十六宫格、圆形、三角形等图形，九宫格的比较常见，先观察是否每横行、每竖行的和都相等，如果不，一般都是横行或者竖行的三个数字存在递推关系，十二宫格偶尔考到，考虑三个数字的递推关系，十六宫格考虑四个数字的加和。同心圆数列一般都是圈上的四个数字递推成中间圆的数字，四三角形数列，考虑角上的三个数字递推成中间三角形数字等。

　　2、数学运算——容斥原理

　　数学运算部分在广东省省考中一共是10道题，所占比重不小，近几年的难度系数整体处于适中，较国考难度系数小很多，但是这部分题目也是相对较耗时的。所以，在时间有限的情况下，一定优先做简单类的题型。例如：容斥问题。容斥原理这部分内容在省考当中大概每两年考一次的频率，而这部分的考点比较简单，省考常考的是对于容斥原理公式的掌握，考场中看到以下类似的题目可以先做。

　　3、数学运算——植树问题

　　植树问题作为广东省考的一种常考的杂题类型，其常考的知识点为拔树重载，拔树重载问题的核心是：不需要重载的树为两次种树间距公倍数的地方，此类题关键是找到两次种树间距的最小公倍数。清楚这一点之后，考场上就可以轻松把握。

　　4、数学运算——数字特性

　　数字特性法往往不需要直接求出问题的解，而是通过分析题目中数据的性质从而找出问题的答案。掌握这部分的核心是对于基本规律的把握和理解。

　　5、数学运算——赋值法

　　赋值法思想给某个量或某些量赋特殊的值，从而帮助我们解决问题。