行测考试中，排列组合的知识经常会出现，很多考生觉得做题目很难做，头痛不已。但是这些题目也是有规律可循的，下面广东公务员考试网（www.gdgwyw.com）介绍几种排列组合常用的几种解题方法，让你的做题又快又准。

　　【常用方法】

　　优限法：优先安排具有绝对限制条件的元素。

　　捆绑法：解决元素相邻问题，将某几个元素看作一个整体。

　　插空法：解决元素不相邻问题，将不相邻的元素插空。

　　间接法：直接考虑比较复杂时，考虑其对立面。

　　【例题精讲】

　　例：甲乙丙丁戊五个人坐一排，请回答下列问题。

　　(1)甲只坐排头或排尾，有( )种排法。

　　(2)甲乙一定要相邻，有( )种排法。

　　(3)甲乙一定不相邻，有( )种排法。

　　(4)甲乙当中至少有一人在首尾两端，有( )种排法。

　　解析：(1)甲有特殊要求，则先排甲，有2种排法，再排其他人，有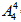=24种，因此所求为2×24=48种。

　　(2)甲乙必须相邻，则将甲乙捆绑在一起看成1个整体，与剩余的3个人进行排列，有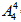=24种，甲乙可以互换顺序，有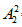=2种，因此所求为24×2=48种。

　　(3)先排另外三个人，有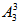=6种，再从这三个人形成的4个空位里选2个安排甲和乙，有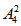=12种，因此所求为6×12=72种。

　　(4)甲乙丙丁戊五个人坐一排共有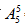=120种，首尾两端没有甲和乙的排法有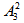×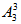=36个，因此所求为120-36=84种。

　　【提升训练】

　　例1：2010年广州亚运会组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作，若其中小张和小赵只能从事前两项工作，其余三人均能从事这四项工作，则不同的选派方案共有( )。

　　A.48种   B.12种   C.18种   D.36种

　　【答案】D。解析：先分类，通过分析可以分成2类：①小张和小赵恰有1人入选，先从两人中选1人，然后把这个人在前两项工作中安排一个，最后剩余的三人进行全排列有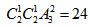种选法。②小张和小赵都入选，首先安排这两人，然后在剩余的3人中选2人排列有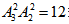种方法。共有24+12=36种选法。

　　例2：某场学术论坛有6家企业作报告，其中A企业和B企业要求在相邻的时间内作报告，C企业作报告的时间必须在D企业之后、在E企业之前，F企业要求不能第一个，也不能最后一个作报告。如满足所有企业的要求，则报告的先后次序共有多少种不同的安排方式?

　　A.12   B.24   C.72   D.144

　　【答案】B。解析：方法一：由题意可知D、C、E的顺序相对固定，要求A、B必须相邻，则将A、B捆绑后插入到D、C、E形成的4个空中有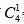=4种方式；因AB内部顺序可以互换有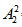=2种方式；又因F不能在第一个，也不能在最后一个，所以F只能安排在AB、D、C、E形成的三个空中有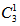=3种方式。则报告的先后次序共有4×2×3=24种不同的安排方式。故本题选B。

　　以上题目对于这四种方法做了简单讲解，各位考生可通过练习达到对每种方法的熟练运用，从而在做题时快人一步。