转眼间2013年春季联考已过去3个月，2014年国考也离我们越来越近。各位考生也应该进入了国考暑期备考的关键阶段，2014年国家公务员考试到底考什么？这是每一个考生都关心的问题。虽然我们无法准确预测每个知识点、每道题会怎么考，但是通过对历年国考大纲的解读以及历年国考的题型变化趋势和2013年全国各地的省考的情况，广东公务员考试网（http://www.gdgwyw.com）为您总结出国考数学运算部分的一些最新的命题趋向和最权威的考点预测，希望对大家的复习备考有所帮助。
分析历年来的国考真题我们发现，国家公务员数学运算部分命题的一个最大趋势是——稳中求变。所谓稳中求变则是在历年必考、常考的题型之上积极尝试、拓展新题型，考查考生的分析解决问题的能力和思维能力，题目变得越来越灵活，死板的方法越来越没有用武之地。而当年国考的命题又受到各省当年省考的一定影响。因此，我们参照以上两方面，对2014年国考的重点题型进行预测——
一、解题思想的综合考查
我们常用的解题思想主要包括：代入排除思想、数字特性思想、方程法思想、赋值法思想等。以上解题思想的常考题型有：多位数问题、余数问题、年龄问题、和差倍比问题、不定方程问题等。历年的国考真题中，对以上解题思想的考查也占据了大量分值。而近年来的国考和省考则趋向于对若干解题思想的综合考查，因此，考生们需要对其引起特别的注意。
热点预测：多种解题思想的综合考查
【例】(2013国家-74)小王参加了五门百分制的测验，每门成绩都是整数。其中语文94分，数学的得分最高，外语的得分等于语文和物理的平均分，物理的得分等于五门的平均分，化学的得分比外语多2分，并且是五门中第二高的得分。问小王的物理考了多少分？( )
A.94 B.95
C.96 D.97
分析：由语文94分，外语为语文和物理的平均分，且每门成绩均为整数可得物理成绩为偶数。排除B、D；将A项94分代入，得到外语为94，化学96，数学大于96，物理94，语文94，平均分不可能为94分。因此，本题答案选择C选项。
【例】举办排球比赛，选男员工的1/11和12名女员工，剩余男员工是剩余女员工的2倍，总员工人数156人，问：男员工有多少人？( )
A. 100 B. 99 C. 111 D. 121
分析：读题之后我们可以迅速发现男员工的人数应该为11的倍数，观查选项，只有B、D两项满足。此时，我们考虑采用代入排除：将B项，男员工99人代入，即第一次选出了9名男员工和12名女员工，因此，剩余90名男员工和156-99-12=45名女员工，满足男员工是女员工2倍这个条件。因此，本题答案为B选项。
小结：这两题题同时考查了数字特性思想和代入排除思想的综合运用，此类题目在今后的国考中成为重点考查对象。并且国考15道数学运算的题目中能够采用数字特性或者代入排除思想的题目一直维持在4道左右，因此，各位考生在备考的过程中一定要能够熟练掌握以及灵活运用这两个解题思想，帮助大家“秒杀”题目。而单一使用一种解题思想“秒杀”出答案的题目将会越来越少。
二、几何问题的新思维、新变化
几何问题是近年来国考数量关系的常考重点题型，题量维持在2道左右。且近几年国考中的几何问题的出题方式也不再局限于传统知识点的考查，更多的是考查考生的思维能力以及解决新题型的能力。因此，考生在备考过程中应对该问题引起足够的重视，做足充分准备，熟悉常考题型及常见解题思路，并且灵活运用基本方法解决新题型。当遇到使用常规思路和解题方法无法解决的问题时，考虑在时间充裕的情况下发散思维，多种角度思考该问题，找到快速的解题方法。
结合历年考查，几何问题不断求变、求新，因此，广东公务员考试网给出以下三道新颖的几何问题，其一为2013年国考压轴题。考生需要认识到：几何问题无论如何变化，其解决方法认识从基本公式、基本知识点入手。
【例】(2013国家-75)若干个相同的立方体摆在一起，前、后、左、右的视图都是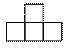
，问这堆立方体最少有多少个？
A.4 B.6 C.10 D.8
【解析】四个正方体如下图摆放，即在“九宫格”的对角线上各摆放一个正方体，再在中心正方体的上方放置一个正方体。左图为立体图，右图为其四向视图。
【预测题目1】如下图所示，在用多边形对平面进行密铺时，相拼接的边相等，每个拼接点处各个角的和为360°，我们称其可以完成平面密铺。那么一下哪种图形不能单独完成平面密铺？
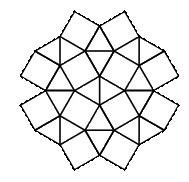
A正三角形 B正方形
C正六边形 D正八边形
分析：很多考生拿到此题后觉得无从下手，仿佛我们从未接触过此类题型。什么是平面密铺？概念很陌生，但是我们只要仔细读题、认真看图后就不难发现：所谓平面密铺，只需满足两个条件，结合所给图示：①正方形和与之拼接的正三角形的边长相等；②每个交点处，正方形和正三角形的各内角和为360°(每个交点处有3个正三角形的内角及2个正方形的内角：3×60°+2×90°=360°)。而题目所求为：只使用一种图形的平面密铺，因此，我们只需考虑以上两个条件即可。显然，只采用一种图形，其对应的拼接边长必然相等；而欲使每个交点处的内角和为360°，由于对于单一正多边形，其每个内角度数相等，因此，只需其内角度数为360°的约数即可，正三角形、正方形、正六边形、正八边形的内角度数分别为，60°、90°、120°、135°，因此正八边形无法单独实现平面密铺。因此，本题答案选择D选项。
小结：本题表面上为几何问题，但实质考查的知识点为约数倍数，是我们很熟悉的一个考点。因此，在解决此类几何问题时，我们需要冷静分析，仔细审题，拨开浓雾，方见彩虹。
【预测题目2】已知图中的三角形均为直角三角形，且三边长度均为整数，正方形ABCD的面积为1平方厘米，那么正方形EFGH的面积为正方形ABCD的多少倍？( )
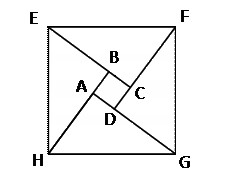
A.10 B.5
C.25 D.12
分析：读题之后，我们发现题目所给的数据量很少，似乎难以求解，但是仔细看图后不难发现，由于图中所有三角形均为直角三角形，我们易证四个直角三角形是全等的(对应角相等，且斜边相等)。因此，由正方形ABCD的面积为1平方厘米，可知正方形ABCD的边长为1厘米，因此，两直角边长度相差1，又三边长度均为整数可知图中直角三角形三边长为3、4、5，因此正方形EFGH的面积为5×5=25平方厘米，为正方形ABCD的25倍。因此，本题答案选择C选项。
小结：本题亦是考查分析解决新问题的典型示例，实质上考查了三角形全等和常见的勾股数，与上一个例题类似，考生们只要冷静分析，结合所学知识点和基本公式，对于此类几何问题是可以很好的解决的。
三、溶液问题：考查饱和溶液的概念
历年国考对于溶液问题都有或多或少的考查，今年也不会例外。而溶液问题的传统题型各位考生在备考过程中也应做好充分的准备，在此我就不进行过多的介绍了。我们需要重点关注的溶液问题的题型是考查饱和溶液，可能部分考生对于此概念还是比较陌生的。因此，我们结合两道例题进行说明：
【例】(安徽2012-62)在某状态下，将28g某种溶质放入99g水中恰好配成饱和溶液，从中取出1/4溶液加入4g溶质和11g水，请问此时浓度变为多少？( )
A. 21.61% B. 22.05% C. 23.53% D. 24.15%
分析：读完题目后可能部分考生就直接拿笔开始计算了，给出了溶质和溶剂质量，求解溶度，很常规的题目。但实际上呢，我们仔细审题后发现，初始溶液已达饱和，而所加的4g溶质和11g水，直接计算浓度的话是大于初始浓度的，而初始溶液已达饱和，也就是说无法溶解更多的溶质，那么加入4g溶质和11g水之后浓度应该与饱和时的浓度相同，即28÷(28+99)=22.05%。因此，本题答案选择B选项。
【例】现有一定浓度的盐水若干克，蒸发一定量的水之后溶液浓度变为20%，在蒸发同样多的水之后浓度变为25%，在蒸发同样多的水之后浓度变为26.5%。那么再蒸发同样多的水之后浓度变为多少？( )
A.26.5% B.30% C.33% D.35%
分析：初看本题，很多考生误以为是传统的等溶质增减类题目，但是稍加计算后发现：由于溶质含量固定，因此每次蒸发同样多的水后，浓度的变化量应该变大，而第三次蒸发后，浓度的变化量为1.5%<5%，说明溶液在第三次蒸发后已变为饱和溶液，因此再次蒸发后浓度应为26.5%。因此，本题答案选择A选项。
小结：以上两道例题均考查了饱和溶液的概念，考生只需记住，在一定条件下，溶液若达到饱和，无论在添加多少溶质，其浓度均不会发生改变。此类题型只要不落入题中设置的陷阱，其难度是远远小于传统浓度问题的。
四、基础题型保持相对稳定
除了以上国考变化的新趋势，国考考查的热点还有相当一部分集中在传统题型上：如典型的行程问题、工程问题、容斥问题、最值问题(需要特殊说明的是；最值问题在近年的考查重点逐步转移到了构造数列问题上，考生需要引起注意)、排列组合问题、和差倍比问题，以上这些考点的考查大多偏向常规题型，考生们只需掌握基本公式和基本解题方法便能应对自如。
结语：结合考试大纲和历年真题，我们发现数学运算部分的考查趋向于基础题型和新题型结合的考查方式，且新题型所占比重不是很大。而且无论题目再怎么创新，其核心和基础的公式不会改变，追根溯源依然是考查我们最基本的知识点。因此，广大考生在复习备考过程中，只有注意传统与创新的结合，夯实基础，，才能不惧创新题型，把握好综合性题型。祝大家一举成“公”。
行测更多解题思路和解题技巧，可参看2014年公务员考试技巧手册。
